Kod untuk blog ini, bersama dengan set data, terdapat di pautan berikut https: // github.com / shekharpandey89 / k-cara
Pengelompokan K-Means adalah algoritma pembelajaran mesin yang tidak diawasi. Sekiranya kita membandingkan algoritma pengelompokan K-Means dengan algoritma yang diawasi, tidak diperlukan untuk melatih model dengan data berlabel. Algoritma K-Means digunakan untuk mengklasifikasikan atau mengelompokkan objek yang berbeza berdasarkan atribut atau ciri mereka menjadi bilangan kumpulan K. Di sini, K adalah nombor bulat. K-Means mengira jarak (menggunakan formula jarak) dan kemudian mencari jarak minimum antara titik data dan kelompok pusat untuk mengklasifikasikan data.
Mari kita fahami K-Means menggunakan contoh kecil menggunakan 4 objek, dan setiap objek mempunyai 2 atribut.
| Objek Objek | Atribut_X | Atribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-Bermakna untuk menyelesaikan Numerasi Contoh:
Untuk menyelesaikan masalah berangka di atas melalui K-Means, kita harus mengikuti langkah-langkah berikut:
Algoritma K-Means sangat mudah. Pertama, kita harus memilih sebarang nombor rawak K dan kemudian memilih pusat atau pusat kluster. Untuk memilih pusat, kita boleh memilih sebilangan objek secara rawak untuk inisialisasi (bergantung pada nilai K).
Langkah asas algoritma K-Means adalah seperti berikut:
- Terus berjalan sehingga tidak ada objek yang bergerak dari pusatnya (stabil).
- Kami mula-mula memilih beberapa centroid secara rawak.
- Kemudian, kami menentukan jarak antara setiap objek dan sentroid.
- Mengumpulkan objek berdasarkan jarak minimum.
Jadi, setiap objek mempunyai dua titik sebagai X dan Y, dan mereka mewakili di ruang grafik seperti berikut:
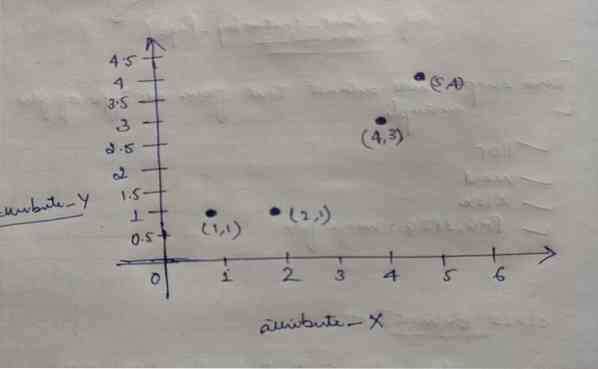
Oleh itu, pada mulanya kami memilih nilai K = 2 secara rawak untuk menyelesaikan masalah kami di atas.
Langkah 1: Pada mulanya, kami memilih dua objek pertama (1, 1) dan (2, 1) sebagai pusat kami. Grafik di bawah menunjukkan sama. Kami memanggil centroid ini C1 (1, 1) dan C2 (2,1). Di sini, kita boleh mengatakan C1 adalah kumpulan_1 dan C2 adalah kumpulan_2.
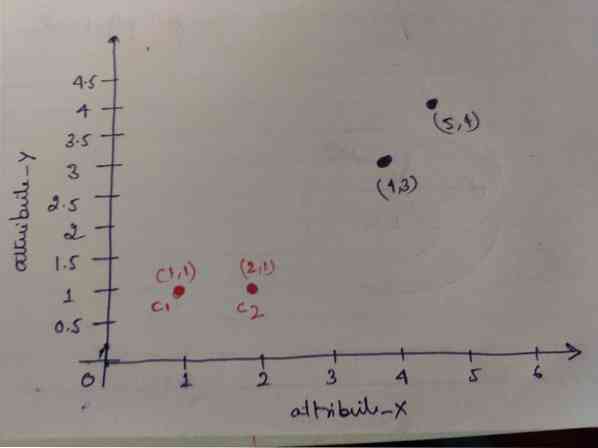
Langkah 2: Sekarang, kita akan mengira setiap titik data objek ke centroid menggunakan formula jarak Euclidean.
Untuk mengira jarak, kami menggunakan formula berikut.

Kami mengira jarak dari objek ke sentroid, seperti yang ditunjukkan dalam gambar di bawah.

Oleh itu, kami mengira setiap jarak titik data objek melalui kaedah jarak di atas, akhirnya mendapat matriks jarak seperti yang diberikan di bawah:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) gugusan1 | kumpulan_1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) gugusan2 | kumpulan_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Sekarang, kami mengira nilai jarak setiap objek untuk setiap centroid. Contohnya, titik objek (1,1) mempunyai nilai jarak ke c1 adalah 0 dan c2 adalah 1.
Seperti, dari matriks jarak di atas, kita mengetahui bahawa objek (1, 1) mempunyai jarak ke kluster1 (c1) adalah 0 dan ke kluster2 (c2) adalah 1. Jadi objek yang satu dekat dengan cluster1 itu sendiri.
Begitu juga, jika kita memeriksa objek (4, 3), jarak ke kluster1 adalah 3.61 dan ke kluster2 adalah 2.83. Jadi, objek (4, 3) akan beralih ke kluster2.
Begitu juga, jika anda memeriksa objek (2, 1), jarak ke kluster1 adalah 1 dan ke kluster2 adalah 0. Jadi, objek ini akan beralih ke kluster2.
Sekarang, mengikut nilai jarak mereka, kami mengelompokkan titik (pengelompokan objek).
G_0 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | kumpulan_1 |
| 0 | 1 | 1 | 1 | kumpulan_2 |
Sekarang, mengikut nilai jarak mereka, kami mengelompokkan titik (pengelompokan objek).
Dan akhirnya, grafik akan kelihatan seperti di bawah setelah melakukan pengelompokan (G_0).
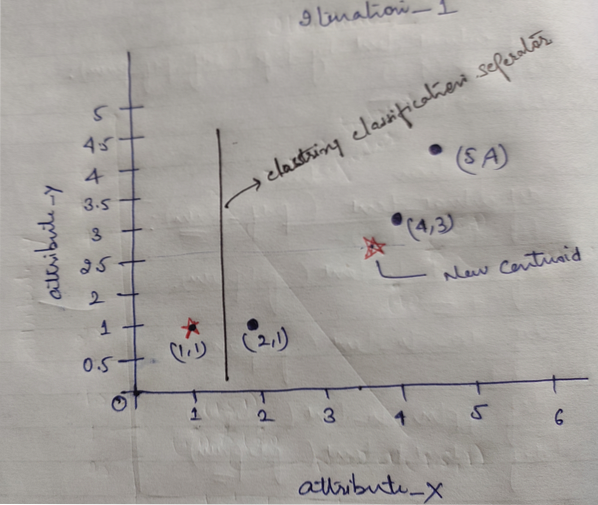
Pengulangan_1: Sekarang, kita akan mengira centroid baru kerana kumpulan awal berubah kerana formula jarak seperti yang ditunjukkan dalam G_0. Jadi, group_1 hanya mempunyai satu objek, jadi nilainya masih c1 (1,1), tetapi group_2 mempunyai 3 objek, jadi nilai centroid barunya adalah 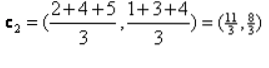
Jadi, baru c1 (1,1) dan c2 (3.66, 2.66)
Sekarang, kita sekali lagi harus mengira semua jarak ke pusat baru seperti yang kita kira sebelumnya.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) gugusan1 | kumpulan_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) gugusan2 | kumpulan_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Iteration_1 (Pengelompokan objek): Sekarang, bagi pihak pengiraan matriks jarak baru (DM_1), kami mengumpulkannya mengikutnya. Jadi, kita mengalihkan objek M2 dari group_2 ke group_1 sebagai peraturan jarak minimum ke centroid, dan objek yang lain akan sama. Jadi pengelompokan baru akan seperti di bawah.
G_1 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | kumpulan_1 |
| 0 | 0 | 1 | 1 | kumpulan_2 |
Sekarang, kita harus mengira centroid baru lagi, kerana kedua objek mempunyai dua nilai.
Jadi, sentroid baru akan menjadi 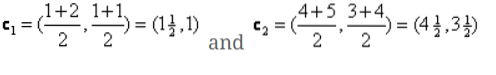
Jadi, setelah kita mendapat centroid baru, pengelompokan akan kelihatan seperti di bawah:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
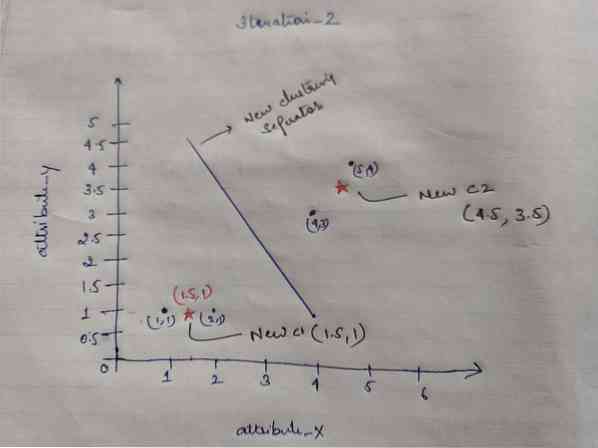
Pengulangan_2: Kami mengulangi langkah di mana kami mengira jarak baru setiap objek ke sentroid baru yang dikira. Jadi, setelah pengiraan, kita akan mendapat matriks jarak berikut untuk iterasi_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) gugusan1 | kumpulan_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) gugusan2 | kumpulan_2 |
A B C D
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Sekali lagi, kami melakukan tugas pengelompokan berdasarkan jarak minimum seperti yang kami lakukan sebelumnya. Jadi setelah melakukannya, kami mendapat matriks pengelompokan yang sama dengan G_1.
G_2 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | kumpulan_1 |
| 0 | 0 | 1 | 1 | kumpulan_2 |
Seperti di sini, G_2 == G_1, jadi tidak perlu lelaran lebih lanjut, dan kita boleh berhenti di sini.
Pelaksanaan K-Means menggunakan Python:
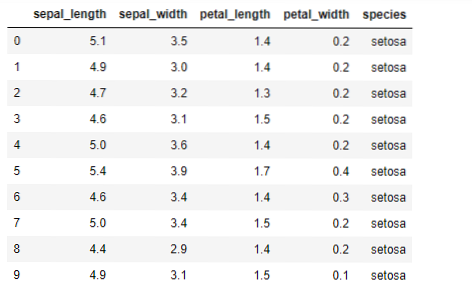
Sekarang, kita akan melaksanakan algoritma K-means di python. Untuk melaksanakan K-berarti, kami akan menggunakan set data Iris yang terkenal, yang merupakan sumber terbuka. Set data ini mempunyai tiga kelas yang berbeza. Set data ini pada asasnya mempunyai empat ciri: Panjang sepal, lebar sepal, panjang kelopak, dan lebar kelopak. Lajur terakhir akan memberitahu nama kelas baris itu seperti setosa.
Set data seperti di bawah:
Untuk pelaksanaan python k-means, kita perlu mengimport perpustakaan yang diperlukan. Jadi kami mengimport Pandas, Numpy, Matplotlib, dan juga KMeans dari sklearn.clutser seperti yang diberikan di bawah:

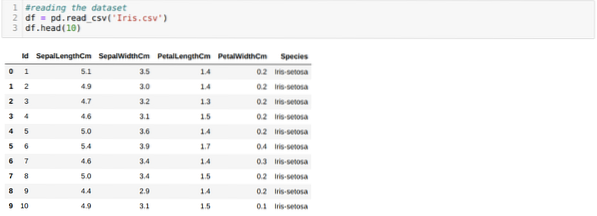
Kami membaca Iris.set data csv menggunakan kaedah read_csv panda dan akan memaparkan 10 hasil teratas menggunakan kaedah kepala.
Sekarang, kami hanya membaca ciri set data yang kami perlukan untuk melatih model tersebut. Oleh itu, kami membaca keempat-empat ciri kumpulan data (panjang sepal, lebar sepal, panjang kelopak, lebar kelopak). Untuk itu, kami meneruskan empat nilai indeks [0, 1, 2, 3] ke fungsi iloc kerangka data panda (df) seperti yang ditunjukkan di bawah:
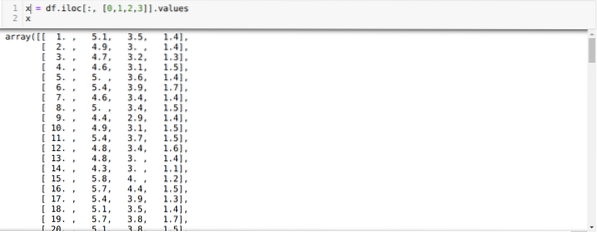
Sekarang, kami memilih bilangan kelompok secara rawak (K = 5). Kami membuat objek kelas K-means dan kemudian memasukkan set data x kami ke dalam untuk latihan dan ramalan seperti yang ditunjukkan di bawah:
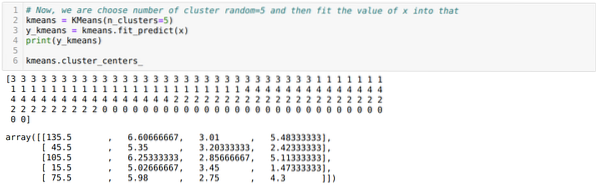
Sekarang, kita akan menggambarkan model kita dengan nilai K = 5 secara rawak. Kami dapat melihat lima kelompok dengan jelas, tetapi nampaknya tidak tepat, seperti yang ditunjukkan di bawah.
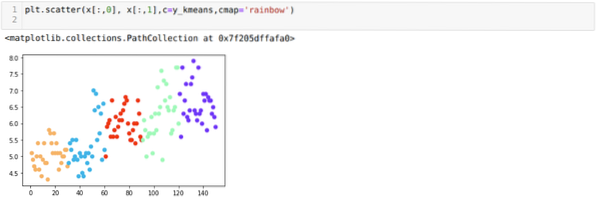
Jadi, langkah seterusnya adalah untuk mengetahui sama ada jumlah kluster itu tepat atau tidak. Dan untuk itu, kami menggunakan kaedah Elbow. Kaedah Elbow digunakan untuk mengetahui bilangan kluster yang optimum untuk set data tertentu. Kaedah ini akan digunakan untuk mengetahui sama ada nilai k = 5 betul atau tidak kerana kita tidak mendapat pengelompokan yang jelas. Jadi selepas itu, kita pergi ke grafik berikut, yang menunjukkan nilai K = 5 tidak betul kerana nilai optimum jatuh antara 3 atau 4.
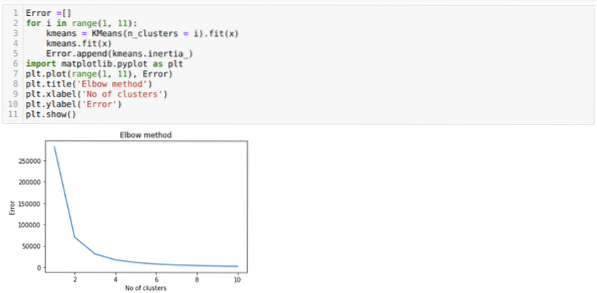
Sekarang, kita akan menjalankan kod di atas sekali lagi dengan bilangan kluster K = 4 seperti yang ditunjukkan di bawah:
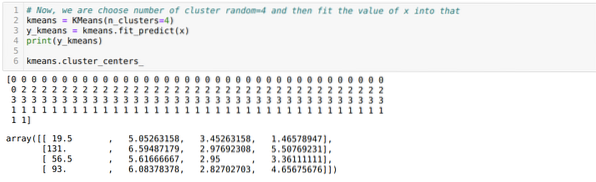
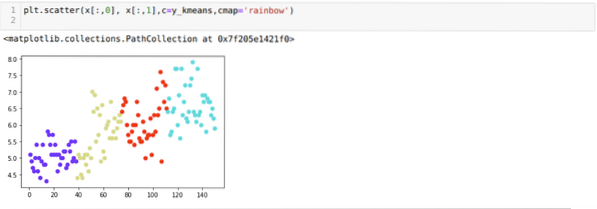
Sekarang, kita akan menggambarkan pengelompokan binaan baru K = 4 di atas. Skrin di bawah menunjukkan bahawa sekarang pengelompokan dilakukan melalui k-means.
Kesimpulannya
Oleh itu, kami mengkaji algoritma K-means dalam kod numerik dan python. Kami juga telah melihat bagaimana kami dapat mengetahui jumlah kluster untuk set data tertentu. Kadang-kadang, kaedah Elbow tidak dapat memberikan jumlah kelompok yang betul, jadi dalam hal ini, ada beberapa kaedah yang dapat kita pilih.
 Phenquestions
Phenquestions


