Perpustakaan NumPy membolehkan kita melakukan pelbagai operasi yang perlu dilakukan pada struktur data yang sering digunakan dalam Pembelajaran Mesin dan Sains Data seperti vektor, matriks dan tatasusunan. Kami hanya akan menunjukkan operasi yang paling biasa dengan NumPy yang digunakan dalam banyak saluran Pembelajaran Mesin. Akhir sekali, harap maklum bahawa NumPy hanyalah cara untuk melaksanakan operasi, jadi, operasi matematik yang kami tunjukkan adalah fokus utama pelajaran ini dan bukan pakej NumPy itu sendiri. Mari kita mulakan.
Apa itu Vektor?
Menurut Google, Vektor adalah kuantiti yang mempunyai arah dan besarnya, terutama untuk menentukan kedudukan satu titik di ruang relatif dengan yang lain.
Vektor sangat penting dalam Pembelajaran Mesin kerana ia tidak hanya menggambarkan besarnya tetapi juga arah ciri. Kita boleh membuat vektor di NumPy dengan coretan kod berikut:
import numpy sebagai npbaris_vektor = np.tatasusunan ([1,2,3])
cetak (baris_vektor)
Dalam coretan kod di atas, kami membuat vektor baris. Kita juga boleh membuat vektor lajur sebagai:
import numpy sebagai npcol_vector = np.tatasusunan ([[1], [2], [3]])
cetak (col_vector)
Membuat Matriks
Matriks hanya dapat difahami sebagai susunan dua dimensi. Kita boleh membuat matriks dengan NumPy dengan membuat susunan pelbagai dimensi:
matriks = np.tatasusunan ([[1, 2, 3], [4, 5, 6], [7, 8, 9]])cetak (matriks)
Walaupun matriks sama dengan tatasusunan pelbagai dimensi, struktur data matriks tidak digalakkan kerana dua sebab:
- Array adalah standard ketika datang ke pakej NumPy
- Sebilangan besar operasi dengan NumPy mengembalikan tatasusunan dan bukan matriks
Menggunakan Matriks Sparse
Untuk mengingatkan, matriks jarang adalah yang mana kebanyakan item adalah sifar. Sekarang, senario biasa dalam pemprosesan data dan pembelajaran mesin adalah memproses matriks di mana sebahagian besar elemen adalah sifar. Sebagai contoh, pertimbangkan matriks yang barisnya menerangkan setiap video di Youtube dan lajur mewakili setiap pengguna yang berdaftar. Setiap nilai menunjukkan sama ada pengguna telah menonton video atau tidak. Sudah tentu, majoriti nilai dalam matriks ini akan menjadi sifar. The kelebihan dengan matriks jarang adalah bahawa ia tidak menyimpan nilai yang sifar. Ini menghasilkan kelebihan komputasi dan pengoptimuman penyimpanan juga.
Mari buat matriks percikan di sini:
dari impor jarangoriginal_matrix = np.tatasusunan ([[1, 0, 3], [0, 0, 6], [7, 0, 0]])
sparse_matrix = jarang.csr_matrix (original_matrix)
cetak (sparse_matrix)
Untuk memahami bagaimana kod berfungsi, kita akan melihat outputnya di sini:
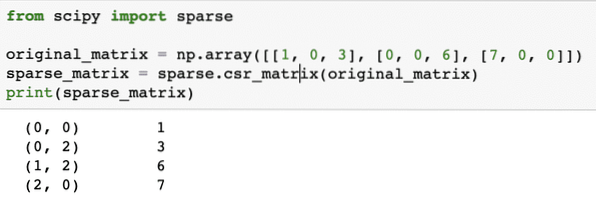
Dalam kod di atas, kami menggunakan fungsi NumPy untuk membuat a Baris jarang yang dimampatkan matriks di mana unsur bukan sifar diwakili menggunakan indeks berasaskan sifar. Terdapat pelbagai jenis matriks jarang, seperti:
- Lajur jarang yang dimampatkan
- Senarai senarai
- Kamus kunci
Kami tidak akan menyelami matriks jarang di sini tetapi tahu bahawa setiap penggunaannya adalah khusus dan tidak ada yang boleh disebut sebagai 'terbaik'.
Menerapkan Operasi ke semua elemen Vektor
Ini adalah senario biasa apabila kita perlu menerapkan operasi bersama pada pelbagai elemen vektor. Ini dapat dilakukan dengan mendefinisikan lambda dan kemudian vektorisasi yang sama. Mari lihat beberapa coretan kod yang sama:
matriks = np.susunan ([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
mul_5 = lambda x: x * 5
vectorized_mul_5 = np.vektor (mul_5)
vektor_mul_5 (matriks)
Untuk memahami bagaimana kod berfungsi, kita akan melihat outputnya di sini:

Dalam coretan kod di atas, kami menggunakan fungsi vektorisasi yang merupakan sebahagian dari perpustakaan NumPy, untuk mengubah definisi lambda sederhana menjadi fungsi yang dapat memproses setiap elemen vektor. Penting untuk diperhatikan bahawa vektorisasi adalah hanya gelung ke atas unsur-unsur dan tidak memberi kesan pada prestasi program. NumPy juga membenarkan penyiaran, yang bermaksud bahawa bukannya kod kompleks di atas, kita hanya boleh melakukan:
matriks * 5Dan hasilnya pasti sama. Saya ingin menunjukkan bahagian yang kompleks terlebih dahulu, jika tidak, anda pasti akan melewatkan bahagian tersebut!
Maksud, Varians dan Sisihan Piawai
Dengan NumPy, mudah melakukan operasi yang berkaitan dengan statistik deskriptif mengenai vektor. Purata vektor dapat dikira sebagai:
np.min (matriks)Varians vektor dapat dikira sebagai:
np.var (matriks)Sisihan piawai vektor dapat dikira sebagai:
np.std (matriks)Output arahan di atas pada matriks yang diberikan diberikan di sini:

Memindahkan Matriks
Transposisi adalah operasi yang sangat biasa yang akan anda dengar setiap kali anda dikelilingi oleh matriks. Transposisi hanyalah cara untuk menukar nilai kolumnar dan baris matriks. Harap maklum bahawa a vektor tidak boleh dialihkan sebagai vektor hanyalah sekumpulan nilai tanpa nilai tersebut dikategorikan menjadi baris dan lajur. Harap maklum bahawa menukar vektor baris menjadi vektor lajur tidak berlaku (berdasarkan definisi aljabar linear, yang berada di luar ruang lingkup pelajaran ini).
Buat masa ini, kita akan mendapat kedamaian hanya dengan memindahkan matriks. Sangat mudah untuk mengakses peralihan matriks dengan NumPy:
matriks.TOutput arahan di atas pada matriks yang diberikan diberikan di sini:
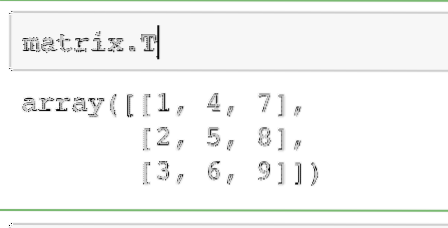
Operasi yang sama dapat dilakukan pada vektor baris untuk mengubahnya menjadi vektor lajur.
Meratakan Matriks
Kita boleh menukar matriks menjadi susunan satu dimensi jika kita ingin memproses unsur-unsurnya secara linear. Ini boleh dilakukan dengan coretan kod berikut:
matriks.ratakan ()Output arahan di atas pada matriks yang diberikan diberikan di sini:

Perhatikan bahawa matriks rata adalah susunan satu dimensi, ringkas dalam fesyen.
Mengira Nilai Eigen dan Eigenvektor
Eigenvektor sangat biasa digunakan dalam pakej Pembelajaran Mesin. Oleh itu, apabila fungsi transformasi linier ditampilkan sebagai matriks, maka X, Eigenvectors adalah vektor yang hanya berubah dalam skala vektor tetapi bukan arahnya. Kita boleh mengatakan bahawa:
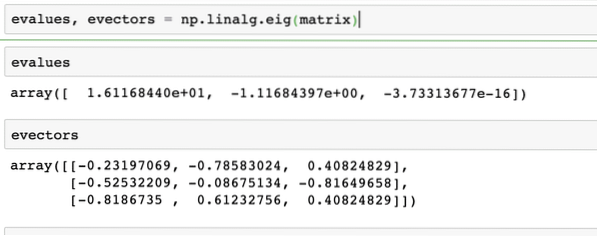
Xv = γvDi sini, X adalah matriks persegi dan γ mengandungi nilai Eigen. Juga, v mengandungi Eigenvectors. Dengan NumPy, mudah untuk mengira Nilai Eigen dan Eigenvektor. Berikut adalah coretan kod di mana kami menunjukkan perkara yang sama:
menilai, evectors = np.linalg.eig (matriks)Output arahan di atas pada matriks yang diberikan diberikan di sini:
Produk Dot Vektor
Dot Products of Vectors adalah cara mengalikan 2 vektor. Ia memberitahu anda mengenai berapa banyak vektor dalam arah yang sama, berbanding dengan produk silang yang memberitahu anda sebaliknya, betapa sedikit vektor berada dalam arah yang sama (disebut ortogonal). Kita dapat mengira titik titik dua vektor seperti yang diberikan dalam coretan kod di sini:
a = np.tatasusunan ([3, 5, 6])b = np.tatasusunan ([23, 15, 1])
np.titik (a, b)
Output arahan di atas pada susunan yang diberikan diberikan di sini:

Menambah, Menolak dan Mengalikan Matriks
Menambah dan Menolak beberapa matriks adalah operasi yang cukup mudah dalam matriks. Terdapat dua cara di mana ini dapat dilakukan. Mari lihat coretan kod untuk menjalankan operasi ini. Untuk tujuan ini, kami akan menggunakan matriks yang sama dua kali:
np.tambah (matriks, matriks)Seterusnya, dua matriks dapat dikurangkan sebagai:
np.tolak (matriks, matriks)Output arahan di atas pada matriks yang diberikan diberikan di sini:
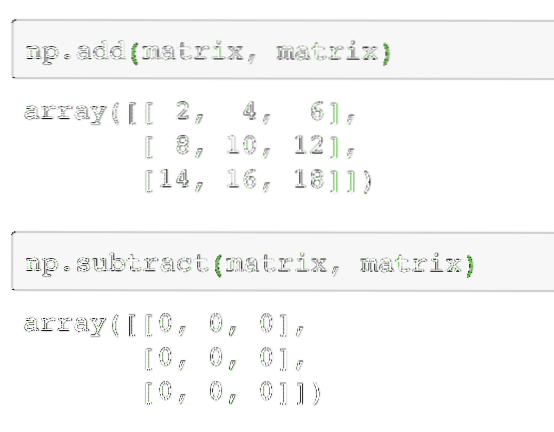
Seperti yang dijangkakan, setiap elemen dalam matriks ditambahkan / dikurangkan dengan elemen yang sesuai. Mengalikan matriks serupa dengan mencari produk titik seperti yang kita lakukan sebelumnya:
np.titik (matriks, matriks)Kod di atas akan menemui nilai pendaraban sebenar dua matriks, yang diberikan sebagai:
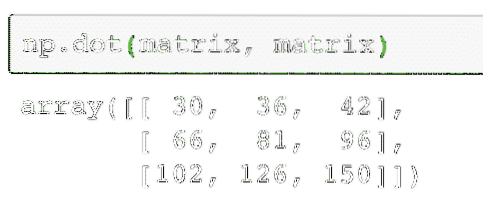
Output arahan di atas pada matriks yang diberikan diberikan di sini:

Kesimpulannya
Dalam pelajaran ini, kami menjalani banyak operasi matematik yang berkaitan dengan Vektor, Matriks dan Susunan yang biasa digunakan Pemprosesan data, statistik deskriptif dan sains data. Ini adalah pelajaran ringkas yang merangkumi bahagian yang paling biasa dan paling penting dari pelbagai konsep tetapi operasi ini harus memberikan idea yang sangat baik tentang semua operasi yang dapat dilakukan ketika berurusan dengan struktur data ini.
Sila kongsi maklum balas anda dengan bebas mengenai pelajaran di Twitter dengan @linuxhint dan @sbmaggarwal (itu saya!).
 Phenquestions
Phenquestions


