Sebagai SciPy adalah sumber terbuka, ia mempunyai komuniti pemaju yang sangat aktif dan bersemangat kerana terdapat banyak modul yang hadir untuk sebilangan besar aplikasi dan pengiraan ilmiah yang tersedia dengan SciPy. Beberapa operasi matematik kompleks yang dapat dilakukan dengan SciPy adalah:
- Interpolasi
- Kesepaduan
- Pengoptimuman
- Pemprosesan imej
- Statistik
- Pengiraan fungsi khas dll.
SciPy dapat dibandingkan dengan kebanyakan perpustakaan perintah dan standard seperti perpustakaan GSL untuk C ++ dan Matlab. Oleh kerana SciPy dibina di atas pakej NumPy, kedua-dua pakej ini dapat disatukan sepenuhnya. Sekiranya anda dapat memikirkan operasi matematik yang perlu dilakukan, pastikan anda memeriksa perpustakaan SciPy sebelum anda melaksanakan modul itu sendiri kerana dalam kebanyakan kes, SciPy mempunyai semua operasi yang telah anda laksanakan sepenuhnya.
Pasang Perpustakaan SciPy
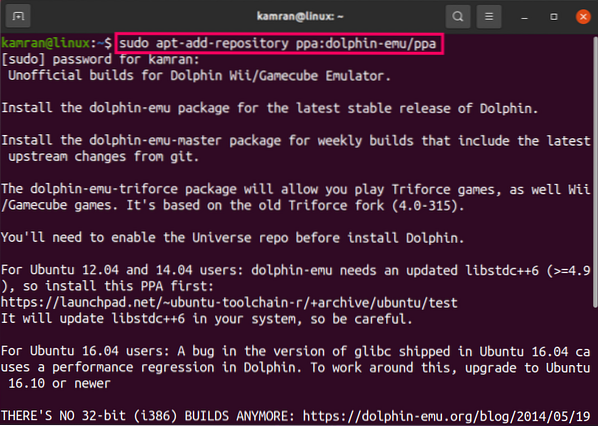
Mari pasang perpustakaan SciPy sebelum kita beralih kepada contoh dan konsep sebenar. Terdapat dua cara untuk memasang pakej ini. Yang pertama termasuk menggunakan pengurus pakej Python, pip:
memasang pip scipyCara kedua berkaitan dengan Anaconda, kita dapat memasang pakej sebagai:
conda install -c anaconda scipySetelah perpustakaan dipasang, kita dapat mengimportnya sebagai:
import scipyAkhirnya, kerana kami juga akan menggunakan NumPy (Disarankan agar untuk semua operasi NumPy, kami menggunakan NumPy secara langsung dan bukannya melalui pakej SciPy):
import numpyAda kemungkinan bahawa dalam beberapa kes, kita juga ingin memplot hasil yang mana kita akan menggunakan perpustakaan Matplotlib. Lakukan import berikut untuk pustaka itu:
import matplotlibSaya akan menggunakan pengurus Anaconda untuk semua contoh dalam pelajaran ini. Saya akan melancarkan Notebook Jupyter untuk perkara yang sama:

Sekarang kita sudah siap dengan semua pernyataan import untuk menulis beberapa kod, mari kita mula menyelami pakej SciPy dengan beberapa contoh praktikal.
Bekerja dengan Persamaan Polinomial
Kita akan mulakan dengan melihat persamaan Polinomial sederhana. Terdapat dua cara untuk menggabungkan fungsi Polynomial ke dalam program kami. Kita boleh memanfaatkan poli1d kelas yang menggunakan pekali atau punca polinomial untuk memulakan polinomial. Mari lihat contoh:
dari numpy import poly1dfirst_polynomial = poly1d ([3, 4, 7])
cetak (first_polynomial)
Apabila kita menjalankan contoh ini, kita akan melihat output berikut:

Jelas, perwakilan polinomial dari persamaan dicetak sebagai output sehingga hasilnya cukup mudah difahami. Kita boleh melakukan pelbagai operasi pada polinomial ini juga, seperti segi empat sama, mencari turunannya atau menyelesaikannya dengan nilai x. Mari cuba lakukan semua ini dalam contoh seterusnya:
cetak ("Polynomial Square: \ n")cetak (first_polynomial * first_polynomial)
cetak ("Derivatif Polinomial: \ n")
cetak (first_polynomial.terbitan ())
cetak ("Menyelesaikan Polinomial: \ n")
cetak (first_polynomial (3))
Apabila kita menjalankan contoh ini, kita akan melihat output berikut:
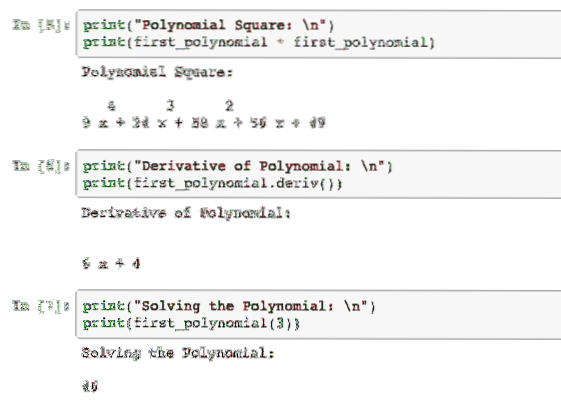
Ketika saya berfikir bahawa ini yang dapat kita lakukan dengan SciPy, saya teringat bahawa kita juga dapat mengintegrasikan Polynomial. Mari jalankan contoh terakhir dengan Polinomial:
cetak ("Mengintegrasikan Polinomial: \ n")cetak (first_polynomial.integ (1))
Bilangan bulat yang kita lalui memberitahu pakej berapa kali untuk mengintegrasikan polinomial:
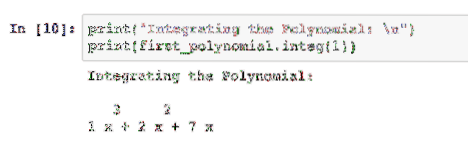
Kita boleh lulus bilangan bulat lain yang memberitahu pakej berapa kali untuk mengintegrasikan polinomial ini.
Menyelesaikan Persamaan Linear
Bahkan mungkin untuk menyelesaikan persamaan linear dengan SciPy dan mencari akarnya, jika ada. Untuk menyelesaikan persamaan linear, kami mewakili set persamaan sebagai tatasusunan NumPy dan penyelesaiannya sebagai tatasusunan NumPy yang berasingan. Mari kita gambarkan dengan contoh di mana kita melakukan perkara yang sama dan memanfaatkannya linalg pakej untuk mencari punca persamaan, berikut adalah persamaan yang akan kita selesaikan:
1x + 5y = 63x + 7y = 9
Mari selesaikan persamaan di atas:
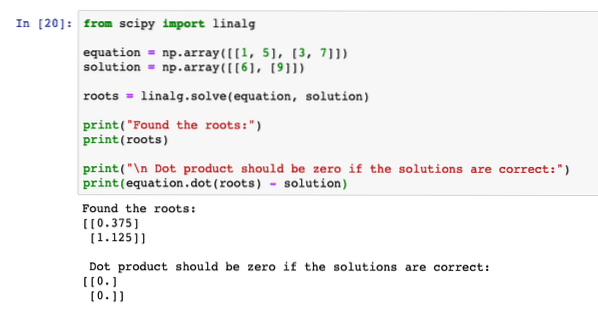
dari linalg import scipypersamaan = np.tatasusunan ([[1, 5], [3, 7]])
penyelesaian = np.tatasusunan ([[6], [9]])
akar = linalg.selesaikan (persamaan, penyelesaian)
cetak ("Menemukan akar:")
mencetak (akar)
cetak ("\ n Produk titik hendaklah sifar jika penyelesaiannya betul:")
mencetak (persamaan.titik (akar) - penyelesaian)
Apabila kita menjalankan program di atas, kita akan melihat bahawa persamaan produk titik memberikan hasil sifar, yang bermaksud bahawa akar yang dijumpai oleh program itu betul:
Transformasi Fourier dengan SciPy
Transformasi Fourier membantu kita mengekspresikan fungsi sebagai komponen berasingan yang membentuk fungsi itu dan membimbing kita tentang cara kita dapat menggabungkan semula komponen tersebut untuk mendapatkan kembali fungsi asal.
Mari kita lihat contoh ringkas Transformasi Fourier di mana kita merancang jumlah dua kosinus menggunakan perpustakaan Matplotlib:
dari scipy.fftpack import fft# Bilangan titik sampel
N = 500
# jarak sampel
T = 1.0/800.0
x = np.ruang lintang (0.0, N * T, N)
y = np.cos (50.0 * 2.0 * np.pi * x) + 0.5 * np.cos (80).0 * 2.0 * np.pi * x)
yf = fft (y)
xf = np.ruang lintang (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib untuk tujuan merancang
import matplotlib.pyplot sebagai plt
plt.plot (xf, 2.0 / N * np.abs (yf [0: N // 2]))
plt.tajuk ('Maklumat')
plt.ylabel ('Paksi Y')
plt.xlabel ('Paksi X')
plt.grid ()
plt.tunjuk ()
Di sini, kita mulakan dengan membina ruang sampel dan persamaan kosinus yang kemudian kita ubah dan plotkan. Berikut adalah output program di atas:
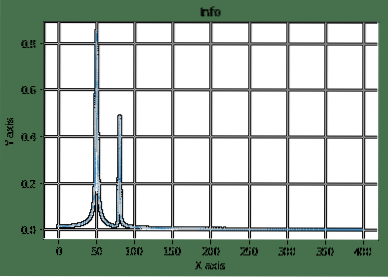
Ini adalah salah satu contoh yang baik di mana kita melihat SciPy digunakan dalam persamaan matematik yang kompleks untuk menggambarkan sesuatu dengan mudah.
Vektor dan Matriks dengan SciPy
Setelah mengetahui banyak perkara yang mampu dilakukan oleh SciPy, kita dapat yakin bahawa SciPy juga dapat bekerja dengan Vektor dan Matriks. Matriks adalah bahagian penting dari aljabar linear kerana matriks adalah sesuatu yang kita gunakan untuk mewakili pemetaan Vektor juga.
Sama seperti kita melihat penyelesaian persamaan linear dengan SciPy, kita dapat mewakili vektor dengan np.susunan () fungsi. Mari mulakan dengan membina matriks:
my_matrix = np.matriks (np.rawak.rawak ((3, 3)))cetak (my_matrix)
Berikut adalah hasil coretan di atas:

Setiap kali kita bercakap mengenai matriks, kita selalu bercakap mengenai Eigenvalues dan Eigenvectors. Dengan kata mudah, Eigen vektor adalah vektor yang, apabila dikalikan dengan matriks, tidak mengubah arahnya, berbanding dengan kebanyakan vektor. Ini bermaksud bahawa walaupun anda mengalikan Eigen vektor dengan matriks, terdapat nilai (atau nilai eigen) yang merupakan salah satu faktor pendaraban. Ini bermaksud:
Ax = λx.Dalam persamaan di atas, A adalah matriks, λ adalah Nilai Eigen dan x adalah Vektor. Mari tulis coretan kod mudah untuk mencari nilai Eigen untuk Vektor yang diberikan:
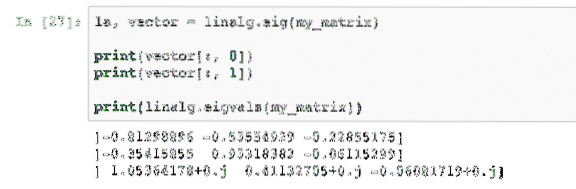
la, vektor = linalg.eig (my_matrix)cetak (vektor [:, 0])
cetak (vektor [:, 1])
mencetak (linalg.eigvals (my_matrix))
Apabila kita menjalankan contoh ini, kita akan melihat output berikut:
Mengira Matriks Penentu
Operasi seterusnya yang akan kita laksanakan dengan SciPy adalah mengira penentu matriks 2 dimensi. Kami akan menggunakan semula matriks yang kami gunakan dalam coretan kod terakhir di sini:
linalg.det (my_matrix)Apabila kita menjalankan contoh ini, kita akan melihat output berikut:

Kesimpulannya
Dalam pelajaran ini, kami melihat banyak contoh yang baik di mana SciPy dapat membantu kami dengan melakukan pengiraan matematik yang kompleks untuk kami dengan API dan pakej yang mudah digunakan.
 Phenquestions
Phenquestions