Tutorial PyTorch dengan Regresi Linear

PyTorch adalah pakej saintifik berasaskan Python yang menyediakan pengganti NumPy ndarrays sebagai Tensor yang memanfaatkan GPU sepenuhnya. Titik positif lain mengenai kerangka kerja PyTorch adalah kelajuan dan fleksibiliti yang diberikannya semasa pengkomputeran. PyTorch adalah alternatif yang berkesan untuk bekerja dengan Tensors menggunakan Tensorflow yang telah kami kaji sebelumnya.

PyTorch mempunyai beberapa kelebihan besar sebagai pakej pengiraan, seperti:

Kita boleh membina grafik pengiraan semasa kita pergi. Ini bermaksud bahawa tidak perlu mengetahui terlebih dahulu mengenai keperluan memori grafik. Kita boleh membuat rangkaian neural dengan bebas dan mengevaluasinya semasa menjalankan.
API Easy to Python yang mudah disatukan
Disokong oleh Facebook, jadi sokongan masyarakat sangat kuat
Memberi sokongan multi-GPU secara semula jadi

PyTorch terutama dipeluk oleh komuniti Sains Data kerana kemampuannya untuk menentukan rangkaian saraf dengan mudah. Mari kita lihat pakej pengiraan ini dalam pelajaran ini.

Memasang PyTorch

Sekadar catatan sebelum memulakan, anda boleh menggunakan persekitaran maya untuk pelajaran ini yang boleh kita buat dengan arahan berikut:

python -m virtualenv pytorch
sumber pytorch / bin / aktifkan

Setelah persekitaran maya aktif, anda boleh memasang perpustakaan PyTorch dalam env maya sehingga contoh yang kami buat seterusnya dapat dilaksanakan:

pip memasang pytorch

Kami akan memanfaatkan Anaconda dan Jupyter dalam pelajaran ini. Sekiranya anda ingin memasangnya di mesin anda, lihat pelajaran yang menerangkan “Cara Memasang Anaconda Python di Ubuntu 18.04 LTS ”dan kongsi maklum balas anda sekiranya anda menghadapi sebarang masalah. Untuk memasang PyTorch dengan Anaconda, gunakan arahan berikut di terminal dari Anaconda:

conda install -c pytorch pytorch

Kami melihat sesuatu seperti ini semasa kami melaksanakan perintah di atas:

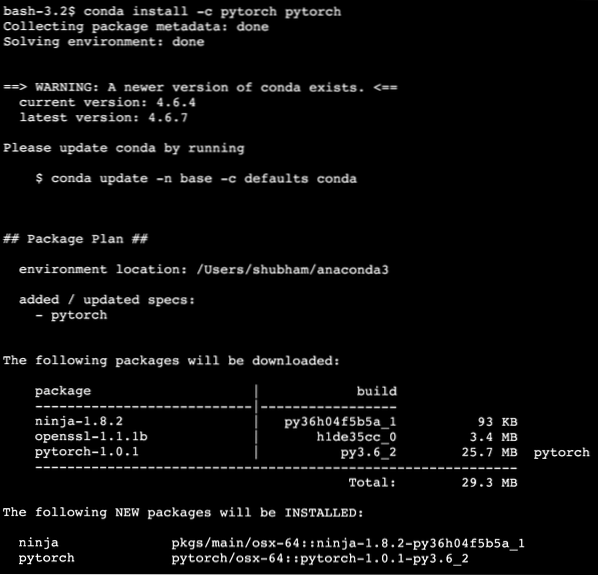
Setelah semua pakej yang diperlukan dipasang dan selesai, kita dapat mulai menggunakan perpustakaan PyTorch dengan pernyataan import berikut:

obor import

Mari mulakan dengan contoh asas PyTorch sekarang kerana kami telah memasang pakej prasyarat.

Bermula dengan PyTorch

Seperti yang kita ketahui bahawa rangkaian saraf dapat disusun secara mendasar karena Tensors dan PyTorch dibangun di sekitar tensor, ada peningkatan yang signifikan dalam prestasi. Kami akan memulakan dengan PyTorch dengan memeriksa terlebih dahulu jenis Tensor yang disediakannya. Untuk memulakannya, import pakej yang diperlukan:

obor import

Seterusnya, kita dapat menentukan Tensor yang belum dimulakan dengan ukuran yang ditentukan:

x = obor.kosong (4, 4)
cetak ("Jenis Array: ".format (x.taip)) # jenis
cetak ("Bentuk Array: ".format (x.bentuk)) # bentuk
cetak (x)

Kami melihat sesuatu seperti ini semasa kami melaksanakan skrip di atas:

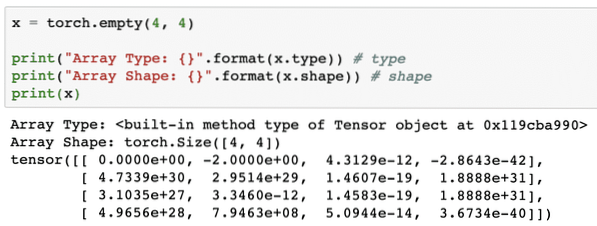
Kami baru saja membuat Tensor yang belum dimulakan dengan ukuran yang ditentukan dalam skrip di atas. Untuk mengulangi dari pelajaran Tensorflow kami, tensor boleh diistilahkan sebagai susunan n-dimensi yang membolehkan kita mewakili data dalam dimensi yang kompleks.

Mari kita jalankan contoh lain di mana kita memulakan tensor Torched dengan nilai rawak:

random_tensor = obor.rand (5, 4)
cetak (rawak_tensor)

Apabila kita menjalankan kod di atas, kita akan melihat objek tensor rawak dicetak:

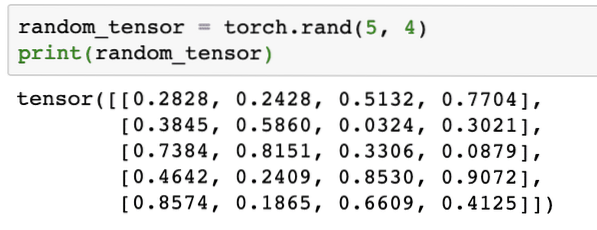
Harap maklum bahawa output untuk Tensor rawak di atas boleh berbeza bagi anda kerana, ia adalah rawak !

Penukaran antara NumPy dan PyTorch

NumPy dan PyTorch benar-benar serasi antara satu sama lain. Oleh sebab itu, mudah untuk menukar tatasusunan NumPy menjadi tegangan dan sebaliknya. Selain kemudahan yang disediakan oleh API, mungkin lebih mudah untuk menggambarkan tensor dalam bentuk tatasusunan NumPy dan bukannya Tensor, atau sebut saja cinta saya untuk NumPy!

Sebagai contoh, kami akan mengimport NumPy ke dalam skrip kami dan menentukan susunan rawak mudah:

import numpy sebagai np
tatasusunan = np.rawak.rand (4, 3)
transformed_tensor = obor.from_numpy (susunan)
cetak (" \ n".format (transformer_tensor))

Apabila kita menjalankan kod di atas, kita akan melihat objek tensor yang diubah dicetak:

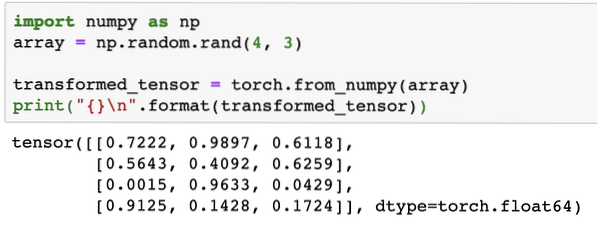
Sekarang, mari kita cuba menukar tensor ini menjadi array NumPy:

numpy_arr = berubah_tensor.numpy ()
cetak (" \ n".format (jenis (numpy_arr), numpy_arr))

Apabila kita menjalankan kod di atas, kita akan melihat array NumPy yang diubah dicetak:

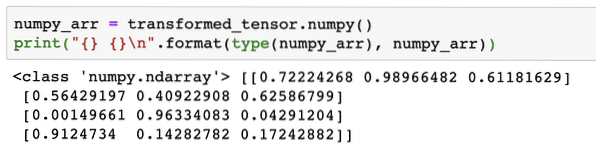
Sekiranya kita melihat dengan teliti, ketepatan penukaran tetap dipertahankan semasa menukar array menjadi tensor dan kemudian menukarnya kembali ke array NumPy.

Operasi Tensor

Sebelum memulakan perbincangan mengenai rangkaian saraf, kita harus mengetahui operasi yang dapat dilakukan pada Tensor ketika melatih rangkaian saraf. Kami juga akan menggunakan modul NumPy secara meluas.

Memotong Tensor

Kami sudah melihat bagaimana membuat Tensor baru, mari buat sekarang dan sekarang kepingan ia:

vektor = obor.tensor ([1, 2, 3, 4, 5, 6])
cetak (vektor [1: 4])

Coretan kod di atas akan memberi kami output berikut:

tensor ([2, 3, 4])

Kita boleh mengabaikan indeks terakhir:

cetak (vektor [1:])

Dan kami akan mendapatkan kembali apa yang diharapkan dengan senarai Python juga:

tensor ([2, 3, 4, 5, 6])

Membuat Tensor Terapung

Sekarang mari kita buat Tensor terapung:

float_vector = obor.FloatTensor ([1, 2, 3, 4, 5, 6])
cetak (float_vector)

Coretan kod di atas akan memberi kami output berikut:

tensor ([1., 2., 3., 4., 5., 6.])

Jenis Tensor ini adalah:

cetak (float_vector.dtaip)

Memberi kembali:

obor.terapung32

Operasi Aritmetik pada Tensor

Kita boleh menambah dua tensor seperti elemen matematik seperti:

tensor_1 = obor.tensor ([2, 3, 4])
tensor_2 = obor.tensor ([3, 4, 5])
tensor_1 + tensor_2

Coretan kod di atas akan memberi kami:

Kita boleh membiak tensor dengan skalar:

tensor_1 * 5

Ini akan memberi kita:

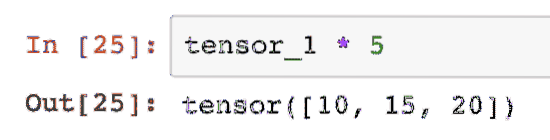
Kita boleh melakukan a produk dot antara dua tensor juga:

d_product = obor.titik (tensor_1, tensor_2)
d_produk

Coretan kod di atas akan memberi kami output berikut:

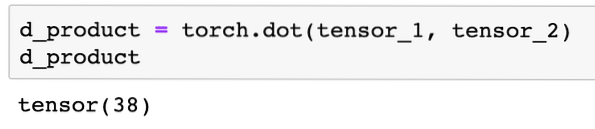
Pada bahagian seterusnya, kita akan melihat dimensi Tensor dan matriks yang lebih tinggi.

Pendaraban Matriks

Dalam bahagian ini, kita akan melihat bagaimana kita dapat menentukan metrik sebagai tensor dan mengalikannya, seperti yang biasa kita lakukan dalam matematik sekolah menengah.

Kami akan menentukan matriks untuk bermula dengan:

matriks = obor.tensor ([1, 3, 5, 6, 8, 0]).pandangan (2, 3)

Dalam coretan kod di atas, kami menentukan matriks dengan fungsi tensor dan kemudian ditentukan dengan fungsi pandangan bahawa ia harus dibuat sebagai tensor 2 dimensi dengan 2 baris dan 3 lajur. Kami dapat memberikan lebih banyak hujah kepada pandangan berfungsi untuk menentukan lebih banyak dimensi. Hanya ambil perhatian bahawa:

kiraan baris didarab dengan jumlah lajur = kiraan item

Apabila kita melihat tensor 2 dimensi di atas, kita akan melihat matriks berikut:

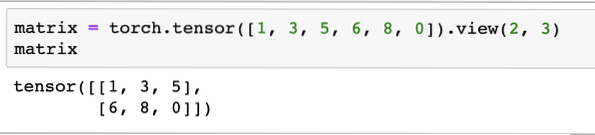
Kami akan menentukan matriks yang serupa dengan bentuk yang berbeza:

matrix_b = obor.tensor ([1, 3, 5, 6, 8, 0]).pandangan (3, 2)

Kami akhirnya dapat melakukan pendaraban sekarang:

obor.matmul (matriks, matriks_b)

Coretan kod di atas akan memberi kami output berikut:

Regresi Linear dengan PyTorch

Regresi linier adalah algoritma pembelajaran mesin berdasarkan teknik pembelajaran yang diawasi untuk melakukan analisis regresi pada pemboleh ubah bebas dan bersandar. Keliru sudah? Marilah kita mendefinisikan Regresi Linear dengan kata mudah.

Regresi linier adalah teknik untuk mengetahui hubungan antara dua pemboleh ubah dan meramalkan berapa banyak perubahan dalam pemboleh ubah bebas menyebabkan berapa banyak perubahan pada pemboleh ubah bersandar. Sebagai contoh, algoritma regresi linier dapat diterapkan untuk mengetahui berapa banyak kenaikan harga untuk sebuah rumah ketika kawasannya meningkat dengan nilai tertentu. Atau, berapa tenaga kuda dalam kereta yang ada berdasarkan berat enjinnya. Contoh kedua mungkin terdengar pelik tetapi anda selalu boleh mencuba perkara yang pelik dan siapa yang tahu bahawa anda dapat menjalin hubungan antara parameter ini dengan Regresi Linear!

Teknik regresi Linear biasanya menggunakan persamaan garis untuk mewakili hubungan antara pemboleh ubah bersandar (y) dan pemboleh ubah bebas (x):

y = m * x + c

Dalam persamaan di atas:

m = cerun lengkung
c = bias (titik yang memotong paksi-y)

Sekarang kita mempunyai persamaan yang mewakili hubungan kes penggunaan kita, kita akan berusaha menyiapkan beberapa sampel data bersama dengan visualisasi plot. Berikut adalah contoh data harga rumah dan ukurannya:

house_prices_array = [3, 4, 5, 6, 7, 8, 9]
rumah_harga_np = np.array (house_prices_array, dtype = np.terapung32)
house_price_np = house_price_np.membentuk semula (-1,1)
house_price_tensor = Pemboleh ubah (obor.dari_numpy (rumah_harga_np))
rumah_saiz = [7.5, 7, 6.5, 6.0, 5.5, 5.0, 4.5]
house_size_np = np.tatasusunan (house_size, dtype = np.terapung32)
house_size_np = house_size_np.membentuk semula (-1, 1)
house_size_tensor = Pemboleh ubah (obor.dari_numpy (house_size_np))
# membolehkan menggambarkan data kami
import matplotlib.pyplot sebagai plt
plt.penyebaran (rumah_harga_susun, rumah_saiz_np)
plt.xlabel ("Harga Rumah $")
plt.ylabel ("Ukuran Rumah")
plt.tajuk ("Harga Rumah $ VS Saiz Rumah")
plt

Perhatikan bahawa kami menggunakan Matplotlib yang merupakan perpustakaan visualisasi yang sangat baik. Baca lebih lanjut mengenainya di Matplotlib Tutorial. Kami akan melihat plot grafik berikut setelah kami menjalankan coretan kod di atas:

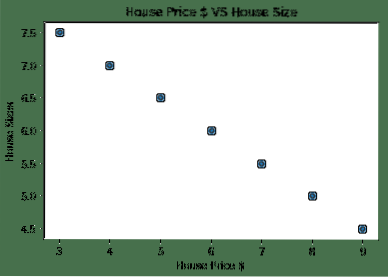
Ketika kita membuat garis besar poin, itu mungkin tidak sempurna tetapi masih cukup untuk jenis hubungan yang dimiliki oleh pemboleh ubah. Setelah kami mengumpulkan dan memvisualisasikan data kami, kami ingin membuat ramalan bahawa berapakah ukuran rumah jika ia dijual dengan harga $ 650,000.

Tujuan menerapkan regresi linier adalah untuk mencari garis yang sesuai dengan data kami dengan ralat minimum. Disini adalah langkah-langkah yang akan kita lakukan untuk menerapkan algoritma regresi linear ke data kami:

Bina kelas untuk Regresi Linear
Tentukan model dari kelas Linear Regression ini
Hitung MSE (Ralat kuasa dua rata-rata)
Lakukan Pengoptimuman untuk mengurangkan ralat (SGD i.e. keturunan kecerunan stokastik)
Lakukan Backpropagation
Akhirnya, buat ramalan

Mari mulakan langkah di atas dengan import yang betul:

obor import
dari obor.pembolehubah import autograd
obor import.nn sebagai nn

Seterusnya, kami dapat menentukan kelas Regresi Linear kami yang mewarisi Modul rangkaian saraf PyTorch:

kelas LinearRegression (nn.Modul):
def __init __ (diri, input_size, output_size):
# fungsi super mewarisi dari nn.Modul supaya kita dapat mengakses segala-galanya dari nn.Modul
super (LinearRegression, self).__di dalamnya__()
# Fungsi linear
diri.linear = nn.Linear (input_dim, output_dim)
def ke hadapan (diri, x):
kembalikan diri.linear (x)

Sekarang kita sudah bersedia dengan kelas, mari tentukan model kami dengan ukuran input dan output 1:

input_dim = 1
output_dim = 1
model = LinearRegression (input_dim, output_dim)

Kita boleh menentukan MSE sebagai:

mse = nn.MSELoss ()

Kami bersedia untuk menentukan pengoptimuman yang dapat dilakukan pada ramalan model untuk prestasi terbaik:

# Pengoptimuman (cari parameter yang mengurangkan ralat)
belajar_kadar = 0.02
pengoptimum = obor.optimis.SGD (model.parameter (), lr = kadar_ pembelajaran)

Kami akhirnya dapat membuat plot untuk fungsi kerugian pada model kami:

loss_list = []
nombor lelaran = 1001
untuk lelaran dalam julat (bilangan iterasi):
# lakukan pengoptimuman dengan kecerunan sifar
pengoptimum.zero_grad ()
hasil = model (house_price_tensor)
kerugian = mse (hasil, ukuran_tensor rumah)
# hitung derivatif dengan melangkah ke belakang
kerugian.ke belakang()
# Mengemas kini parameter
pengoptimum.langkah ()
# kerugian kedai
senarai_ kerugian.tambahkan (kerugian).data)
# kehilangan cetakan
jika (lelaran% 50 == 0):
cetak ('zaman , kerugian '.format (lelaran, kerugian.data))
plt.plot (julat (bilangan_ iterasi), senarai_ rugi)
plt.xlabel ("Bilangan Pengulangan")
plt.ylabel ("Kerugian")
plt

Kami melakukan pengoptimuman berkali-kali pada fungsi kerugian dan cuba membayangkan berapa banyak kerugian yang meningkat atau menurun. Inilah plot yang merupakan output:

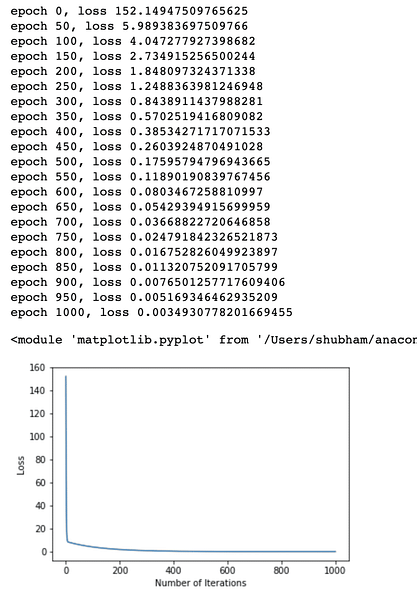
Kami melihat bahawa kerana bilangan lelaran lebih tinggi, kerugian cenderung menjadi sifar. Ini bermaksud bahawa kita sudah bersedia untuk membuat ramalan dan merancangnya:

# ramalkan harga kereta kami
diramalkan = model (house_price_tensor).data.numpy ()
plt.penyebaran (house_prices_array, house_size, label = "data asal", warna = "merah")
plt.penyebaran (house_prices_array, ramalan, label = "data ramalan", warna = "biru")
plt.legenda ()
plt.xlabel ("Harga Rumah $")
plt.ylabel ("Saiz Rumah")
plt.tajuk ("Nilai asal vs Ramalan")
plt.tunjuk ()

Inilah plot yang akan membantu kita membuat ramalan:

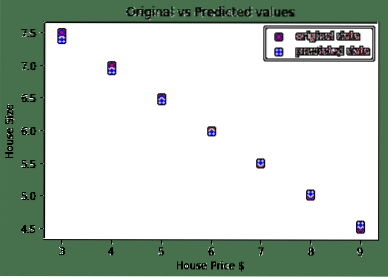
Kesimpulannya

Dalam pelajaran ini, kami melihat pakej pengiraan yang sangat baik yang membolehkan kami membuat ramalan yang lebih pantas dan cekap dan banyak lagi. PyTorch sangat popular kerana cara ini membolehkan kita mengurus rangkaian Neural dengan cara asas dengan Tensors.